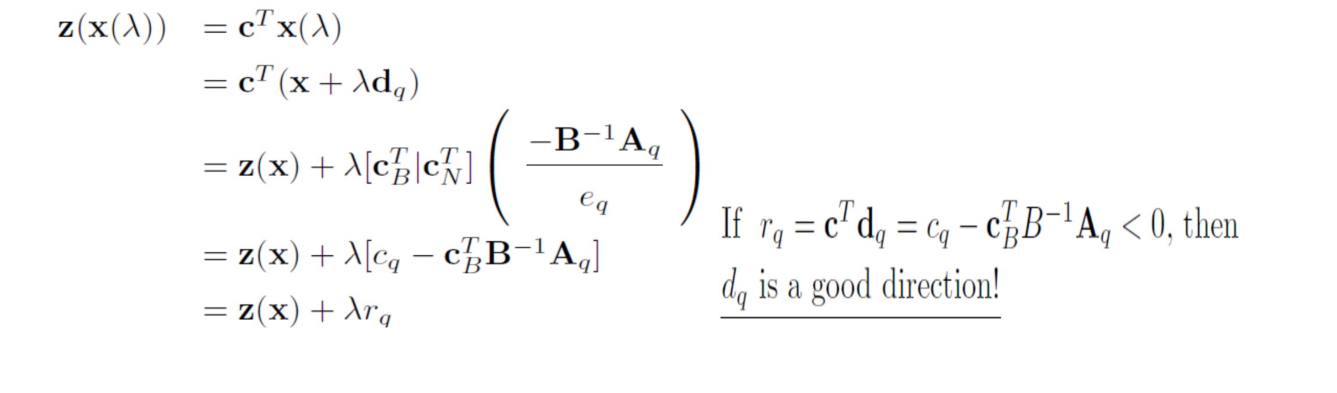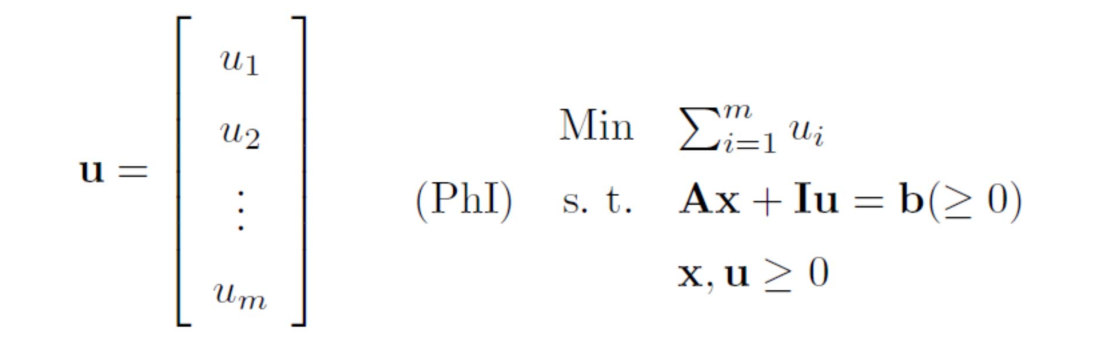前言
——迭代,最好的时代,也是最坏的时代
Phase I:
- 第一步:找初始极点,或发现可行域为空后停止
Phase II:
- 第二步:判断是否最优(关键),是则停止
- 第三步:前往下一个更优点(关键)
该算法迭代最终一定会停止,因为极点的个数不超过$C\left(n,m\right)$,只要不重复,算法一定会停止。
(可跳过)首先我们确定了这样一个算法流程,假定我们能够判断现在所处的极点是否最优,那么如果非最优,我们需要考虑找到一条路前往下一个更理想的点。而这章前一堂课,则集中于讲述如何从一个极点前往其相邻的极点。
在这之前可以观察到一个现象——退化(degeneracy),利用上节求极点的方法,我们有$n-m$个非基变量,有$m$个基变量,非基变量均为0,通过$\mathrm{Bx_B=b}$可以求解出基变量的值,所求基变量的值若均大于0则未出现退化现象,若存在某(些)基变量的值为0,则出现退化现象。为什么会出现退化现象?矩阵A具有哪些特点才会导致出现退化现象?我目前也不知道。从非退化到退化。
但退化现象的存在可能会让我们在上述算法的迭代过程中陷入死循环。为什么?此先搁置,马上揭晓。
让我们回到相邻(adjacency)这个概念,相邻的定义:对于一个极点和它的一个邻居,它们仅有一个基变量和一个非基变量不同,且是该极点的一个非基变量是由0变为正,这个过程称为pivoting,在这个过程中,其他基变量中有一个最先减到0,此时到达了它的邻居。因此不考虑退化,每个极点都存在n-m个邻居。
那么如何前往一个极点的邻居?我们需要找到一个方向向量,沿着该方向可以实现极点的转换,而这个方向蕴藏在矩阵$\mathbf{M}^{-1}$中。这个方向在几何意义上是一条边的方向。关键一点是矩阵M为什么要取逆,有无合理的动力来走到这一步。
回顾时想到的几个问题:
线性规划的可行域一定是凸集吗?——是的,Geometry of LP里面讲过,从定义出发可证明,可行域内任意两点的凸组合仍然在可行域内。
简单回顾:
- 如果可行域非空,则至少有一个vertex(即极点) from Resolution Theorem(可行域内所有点可由vertex的凸组合(加extreme vector)表示);
- 如果可行域非空且目标值有界,则线性规划问题可在一个或多个vertex上取到最优值 from Fundamental Theorem(可行域非空则最优值要么是负无穷,要么在极点处取到)。
- 可行域有有限个vertex,$C\left(n, m\right)$;
- Vertex可通过basic feasible solution生成。
因此,如果$C\left(n,m\right)$很小,我们可以通过枚举法找出所有basic feasible solution,但如果$C\left(n,m\right)$很大的话,枚举法效率很低,因此引出了单纯形法。
Nondegeneracy and adjacency
\[\mathbf{Ax=b}\\ \mathbf{A}=\left[\mathbf{B}\mid \mathbf{N}\right] \\ \mathbf{x} = \left[ \begin{array}{c} \mathbf{x_B} \\ \mathbf{x_N} \end{array} \right],\\ \mathbf{x_N}=\mathbf{0},\ \mathbf{x}\ge0\]设置$\mathbf{x}_N$为0,可以算出一个basic solution $\mathbf{x}_B=\mathrm{B^{-1}}\mathbf{b}$,若$\mathbf{x}_B\ge 0$则$\mathbf{x}$是basic feasible solution,也是一个极点。那当我们从一个bfs移动到另一个bfs时,我们是否也在从一个极点移动到另一个极点?
回顾一下,我们求解bfs时是令$n-m$维为0,若出现退化现象(即所求$\mathbf{x}_B$中有元素等于0),则存在情况:令$\mathbf{x}$的不同于刚才的$n-m$维为0,最后得到的$\mathbf{x}$与刚才求到的$\mathbf{x}$相同,即同一个极点,此时则可能会陷入死循环。此时同一个极点对应了多个不同的bfs,即该bfs为degenerate。
同一个极点对应多个不同的bfs,但本质上这些bfs都是同一个向量。
退化定义:
- If an extreme point is determined by a bfs with exactly m positive basic variables and n-m zero non-basic variables, then the correspondence is one-to-one.
- Only when there exists at least one basic variable becoming 0, then the extreme point may correspond to more than one bfs.
如果每一个bfs均为非退化,则该线性规划问题也是非退化的。
如果一个basic feasible solution是非退化的,则$\mathbf{x}$由n个超平面唯一决定(n-m个变量等于0以及m个等式约束)。
\[\mathbf{A}=\left[\mathbf{B}\mid \mathbf{N}\right],\ \mathbf{x} = \left[ \begin{array}{c} \mathbf{x_B} \\ \mathbf{x_N} \end{array} \right]= \left[ \begin{array}{c} \mathbf{B}^{-1}\mathbf{b} \\ \mathbf{0} \end{array} \right] \\ let\ \mathbf{M} = \left[ \begin{array}{cc} \mathbf{B} & \mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right], \ \mathbf{M}\ is\ nonsingular \\ \mathbf{Mx} = \left[ \begin{array}{cc} \mathbf{B} & \mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right] \left[ \begin{array}{c} \mathbf{x_B} \\ \mathbf{x_N} \end{array} \right]= \left[ \begin{array}{c} \mathbf{b}\\ \mathbf{0} \end{array} \right]\\ \mathbf{x} = \left[ \begin{array}{c} \mathbf{x_B} \\ \mathbf{x_N} \end{array} \right]=\mathbf{M}^{-1} \left[ \begin{array}{c} \mathbf{b}\\ \mathbf{0} \end{array} \right]\\ \mathbf{M}^{-1} = \left[ \begin{array}{cc} \mathbf{B}^{-1} & -\mathbf{B}^{-1}\mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right]\]$\mathbf{M}^{-1}$或者$\mathbf{M}$被称为线性规划问题的基本矩阵(fundamental matrix)
如果一个basic feasible solution是退化的,则$\mathbf{x}$是由超过n个超平面over-determined。
除了上述n个超平面,至少存在一个基变量$x_i=0$(也是一个超平面)。
疑问:$x_i=0$不也是由$\mathbf{Bx=b}$决定的的吗?为什么会多一个超平面?
若退化的basic feasible solution含有p个正数元素(p<m),则至多又$C\left(n-p, n-m\right)$个不同的bfs对应同一个极点。
相邻
如果两个basic feasible solution有m-1个基变量相同,则称它们相邻。无退化的情况下,每个bfs有n-m个相邻邻居。并且可以通过令一个非基变量从0开始增加直至一个基变量减少至0。
Simplex method under nondegeneracy
Nondegeneracy表明极点与bfs一一对应。那么如何进行相邻bfs的转换,如何找到转换的方向向量。无退化的情况下,每个bfs有$n-m$个相邻邻居。并且可以通过令一个非基变量从0开始增加直至一个基变量减少至0。
Who and where are my neighbors?
$x_1 = x_0 +\lambda \mathbf{d}_q,\ \lambda>0$,$\mathbf{d}_q$为edge direction,作用是使得仅某一个非基变量逐渐增大,直至使得一个基变量减少为0。那么如何找到所有($n-m$个)edge directions呢?
从fundemental matrix $\mathbf{M}$知在nondegeneracy情况下, \(\mathbf{x} = \left[ \begin{array}{c} \mathbf{x_B} \\ \mathbf{x_N} \end{array} \right]=\mathbf{M}^{-1} \left[ \begin{array}{c} \mathbf{b}\\ \mathbf{0} \end{array} \right]\\ \mathbf{M}^{-1} = \left[ \begin{array}{cc} \mathbf{B}^{-1} & -\mathbf{B}^{-1}\mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right]\) 刚好 \(\left[\begin{array}{c} -\mathbf{B}^{-1}\mathbf{N} \\ \mathbf{I} \end{array}\right]\) 为$n\times(n-m)$维度,是否$ \mathbf{d}_q $ 可以从该矩阵的$n-m$列中求得,其中$\mathbf{N=[A_{q1},A_{q2},\cdots,A_{q(n-m)}]}$,故先假设
\(\mathbf{d}_q=\left[\begin{array}{c} -\mathbf{B}^{-1}\mathbf{A}_q \\ 0 \\ \vdots \\ 1\\ \vdots \\ 0 \\ \end{array}\right]\)。
所以$x_1 = x_0 +\lambda \mathbf{d}_q=[\begin{array}{c}\mathbf{x_B} \ \mathbf{x_N}\end{array}]+\lambda \left[\begin{array}{c} -\mathbf{B}^{-1}\mathbf{A}_q \ e_q \end{array}\right]$,而$\mathbf{Bx_B}+\mathbf{Nx_N}=\mathbf{b}$,所以$\mathbf{x_B}=\mathbf{B^{-1}b}-\mathbf{B^{-1}Nx_N}=\mathbf{B^{-1}b}$,所以$x_1$的基变量部分变为$\mathbf{B^{-1}b}-\lambda\mathbf{B}^{-1}\mathbf{A}_q$,非基变量部分为$\lambda e_q$,也即使得某一非基变量增加,改变基变量部分,从0不断增大$\lambda$直至出现任一基变量减小为0。所以上述假设满足pivoting概念上的要求,但是是否沿该方向前进且未抵达邻居前,$x_1$是否在可行域内?也即$\mathbf{d}_q$是不是feasible edge direction。
在$\lambda$增大的过程中,$\mathbf{A}x_1=\mathbf{A}x_0+\lambda\mathbf{Ad}_q$,而由$\mathbf{MM^{-1}}=I$可得$\mathbf{Ad}_q=\mathbf{0}$,所以$\mathbf{A}x_1=\mathbf{A}x_0+\lambda\mathbf{Ad}_q=\mathbf{A}x_0=\mathbf{b}$,无论$\lambda$为何值$x_1$均满足等式约束。
- 在nondegeneracy情况下,$\mathbf{x_B}>0$,所以对于足够小的$\lambda$,$x_1\ge0$,所以此时$\mathbf{d}_q$是feasible edge direction。
- 在degeneracy情况下,$\mathbf{x_B}$中存在变量等于0,若$\mathbf{d}_q$中对应的元素为负数,因$\lambda>0$,故$x_1$不满足$x_1\ge0$,此时该$\mathbf{d}_q$不是feasible edge direction。
因此,从上述推理过程可得出结论,在nondegeneracy情况下,可以选取
\[\mathbf{d}_q=\left[\begin{array}{c} -\mathbf{B}^{-1}\mathbf{A}_q \\ 0 \\ \vdots \\ 1\\ \vdots \\ 0 \\ \end{array}\right]\]作为edge direction来从当前极点转移至邻居极点。
Which neighbor is a good one?
从上节我们知道在nondegeneracy情况下有$n-m$个feasible edge directions可选,那么选哪一个方向可尽量最优,且保证下一邻居不劣于当前极点。答:不忘初心。
记$\mathbf{x}=\mathbf{x}+\lambda \mathbf{d}_q$、$z\left(\mathbf{x}\left(\lambda\right)\right)=\mathbf{c}^T \mathbf{x}\left(\lambda\right)=\mathbf{c}^T \mathbf{x}+\mathbf{c}^T \mathbf{d}_q$,故我们需要$\mathbf{c}^T\mathbf{d}_q\le 0$,代入计算即可得到符合要求的$\mathbf{d}_q$。下图中$r_d$称为reduced cost。
定理:若$\mathbf{x}$是关于$\mathbf{B}$的basic feasible solution,且对于某一nonbasic variable $x_q$有$r_q>0$,则$\mathbf{d}_q=\left[\begin{array}{c} -\mathbf{B}^{-1}\mathbf{A}_q \ e_q \end{array}\right]\in\mathbf{R}^n$指向更优目标值。
在采用单纯形法时不必强求找到最小的reduced cost,因为无法预知下一步后可找到的最优reduced cost和另一条路相比哪个更好(即贪心算法不一定都好)。
定理:给定关于$\mathbf{B}$的basic feasible solution $\mathbf{x}$,若对于任一nonbasic varible $x_q$都有$r_q\ge0$,则$\mathbf{x}$是最优解。
证明:\(\forall \mathbf{y}\in P, \mathbf{y}=\left(\begin{array}{c}\mathbf{y}_B\\\mathbf{y}_N\end{array}\right)\ge 0, \mathbf{Ay=b}\),而$\mathbf{x}_{N}^{0}=0, \mathbf{A}\mathbf{x}^0=\mathbf{b}$
\[\mathbf{M}\left(\mathbf{y}-\mathbf{x}^0\right) = \left[ \begin{array}{cc} \mathbf{B} & \mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right] \left[ \begin{array}{c} \mathbf{y}_B-\mathbf{x}_B^0 \\ \mathbf{y}_N \end{array} \right]\\ = \left[ \begin{array}{c} 0 \\ \mathbf{y}_N \end{array} \right]\] \[\mathbf{y}-\mathbf{x}^0 = \mathbf{M}^{-1} \left[ \begin{array}{c} 0 \\ \mathbf{y}_N \end{array} \right] = \left[ \begin{array}{cc} \mathbf{B}^{-1} & -\mathbf{B}^{-1}\mathbf{N} \\ \mathbf{0} & \mathbf{I} \end{array} \right] \left[ \begin{array}{c} 0 \\ \mathbf{y}_N \end{array} \right]\\ = \left[ \begin{array}{c} -\mathbf{B}^{-1}\mathbf{N} \mathbf{y}_N \\ \mathbf{y}_N \end{array} \right] = \left[ \begin{array}{c} -\mathbf{B}^{-1}\mathbf{N} \\ \mathbf{I} \end{array} \right] \mathbf{y}_N = \sum_{q\in N} y_q\mathbf{d}_q\]所以,$\mathbf{y} = \mathbf{x}^0+\sum_{q\in N} y_q\mathbf{d}_q$,故$\mathbf{c}^{T}\mathbf{y}\ge \mathbf{c}^{T} \mathbf{x}^0$。
推论1:若对于任一nonbasic varible $x_q$都有$r_q>0$,则关于$\mathbf{B}$的basic feasible solution $\mathbf{x}$是唯一最优解。
推论2:若$\mathbf{x}$是最优basic feasible solution且部分reduced cost为0($r_{q1},r_{q2},\cdots,r_{qk}=0$),则可行域$\mathbf{P}$内满足$\mathbf{y}=\mathbf{x}+\sum_{i=1}^{k}y_{qi}d_{qi}$的点$\mathbf{y}$也是最优解。
在nondegenracy的情况下,若basic feasible solution $\mathbf{x}$是最优解,则对于任一nonbasic variable $x_q$都有$r_q\ge0$。在degenracy的情况下则不一定成立。
How far is my good neighbor?
判断思想:沿feasible edge direction前进过程中首次出现基变量减小为0时停止($\mathbf{d}_q$中至少有一个元素小于0),此时达到neighbor。若无界($\mathbf{d}_q\ge0$),又因$r_q = \mathbf{c}^T\mathbf{d}_q<0$,故一直前进至无穷远。
对于$\mathbf{x}\left(\alpha\right)=\mathbf{x}+\alpha \mathbf{d}_q,\alpha>0$且$r_q = \mathbf{c}^T\mathbf{d}_q<0$
- 针对$\mathbf{d}_q\ge0$,$\mathbf{x}\left(\alpha\right)\ge 0, \forall\alpha\ge0$,故$\mathbf{x}\left(\alpha\right)\in P, \forall\alpha>0$,同时随着$\alpha\rightarrow-\infty$,$\mathbf{c}^{T}\mathbf{x}\left(\alpha\right)=\mathbf{c}^{T}\mathbf{x}+\alpha\mathbf{c}^{T}\mathbf{d}_q\rightarrow -\infty$。
- 针对$\mathbf{d}_q$中至少有一个元素小于0,有$\alpha=\min{\frac{x_i}{-d_{qi}}}>0,d_{qi}<0$,正好完成一个pivoting,$\min{\frac{x_i}{-d_i}}$被称为minimum ratio test。若有多个(两个及以上)basic variables同时变为0,则说明degenerate。
- 若为degenerate情况,则对于$d_{qi}<0$,$x_i$可能为0,此时$\alpha=0$,stuck! trapped into a loop。
至此,我们已经知道了如何判断当前极点是否最优,以及非最优时如何前往下一个极点。所以我们可以完善单纯形法的步骤:
How to start the simplex method?
如何选取初始的basic feasible solution以开启迭代:
- 观察法
- 随机生成,$\left(\begin{array}{c}n\ n-m\end{array}\right)$
- 系统方法
- Two-phase method
- big-M method(不太可靠)
Two-phase method
特点:
$\mathbf{u}=\mathrm{b},\mathbf{x}=0$是(PhI)的一个basic feasible solution。
从此开始迭代即可求解(PhI)。
(PhI)目标值大于等于0。
所以一定可以求到(PhI)的最优解,但是该最优解不一定是原问题的可行解。
原线性规划问题有解当且仅当$\mathbf{z}_{PhI}=0$。
也即一开始时选则$\mathbf{u}$的m个变量作为basic variables,$\mathbf{x}$作为nonbasic variables,然后再迭代过程中不断地使$\mathbf{x}$中元素渗透入basic varibles、$\mathbf{u}$中元素一个个地离开basic varibles。
在nondegeneracy情况下,如果$\mathbf{z}_{PhI}=0$,那么(PhI)的最优解是原线性规划的一个basic feasible solution。
当构造的规划问题的最优解对应的目标值为0时,从该最优解中的$\mathbf{x}$开始迭代即可求解原线性规划问题;若构造的规划问题的最优解对应的目标值大于0,则说明原线性规划问题无解。
在degenerate情况下
若在标准化线性规划问题时处理了redundant case,则第二种情况不会发生。
Two-phase Method在寻找原线性规划的一个basic feasible solution时需先解一个自己构造的、有basic feasible solution的线性规划问题,以得到最优解作为原问题的bfs。
Big-M Method
构造如下问题:
$\mathbf{u}=\mathrm{b},\mathbf{x}=0$是一个初始的basic feasible solution,M是一个很大的数(理论上应该无穷大)。所以该问题有最优解(有限)或趋于负无穷。
该方法解得到的最优解分以下几种情况:
- 最优解为$\left(\begin{array}{c}\mathbf{x}\ \mathbf{u}\end{array}\right)$,$\mathbf{u}=0$,则$\mathbf{x}$是原线性规划问题的最优解;
- 最优解为$\left(\begin{array}{c}\mathbf{x}\ \mathbf{u}\end{array}\right)$,$\mathbf{u}\ne 0$,则原问题无解;
- 目标值趋于负无穷,且$\mathbf{u}=0$,则原线性规划问题也是趋于负无穷;否则原问题无解。
特点:
商业线性规划求解器倾向于使用Two-phase Method。
Preventing cycling for finite termination
首先我们需要知道产生degenerate的原因是什么。我们在选取$\mathbf{d}_q$后,使某一nonbasic variable增加,直至首次出现basic variable减少至0,若同时出现多个basic variable减少到0,则产生了degenerate。
当我们求解的线性问题是degenerate,则容易陷入loop。在进行pivoting时虽然实现了相邻bfs之间的转化,但这两个bfs可能对应着同一个extreme point(在计算过程中体现的是$\alpha=0$,即步长为0,即对应的目标值没有严格减小),并因此可能陷入loop。
为了解决因已产生的degenerate而导致的cycling/loop问题,有图下方法。其中之一是,在出现多个basic variable减少至0时,始终选择下标小的作为nonbasic variable,有序进出以避免degenerate导致的cycling。
用perturbation来避免degenerate,为数值方法,在同时出现多个basic variable减少到0时添加perturbation,来避免degenerate。
Extension: Simplex Method Programming
不妨用MATLAB或Python实现一下Two-phase Method + Simplex Method求解任一线性规划问题。
记住不忘本心,需将输入的线性规划问题转成标准形式,同时检验等式约束方程组是否有线性相关的方程或矛盾的方程。这一步比较关键,虽然技术含量低但是需考虑许多情况。